An article posted today by Marco Ponzi alerted me to some VMS text analyses I have never seen before. A Google search revealed that several researchers have studied vowel placement in natural languages and some of those concepts were used to analyze VMS text (e.g., W.F. Bennett and linguist Jacques Guy).

So I looked up Guy’s papers, read through the first one, and am stating right up front that no matter how often one runs the numbers, vowel-identification analyses on individual glyphs in the VMS is not going to work as it does for natural languages. In this blog, I’ll explain why.

Background

For those interested in computational attacks and historical precedents, here is a summary of my Google search for the VMS-related work of Jacques Guy:

• Cryptologia 1991 (Issue 3), “Statistical Properties of Two Folios of the Voynich Manuscript” by Jacques B. M. Guy, in which he analyzes folios 79v and 80r as to letter frequency in terms of both word and line placement, and co-occurrence, with a “tentative phonetic categorization of letters into vowels and consonants using Sukhotin’s algorithm”. This was republished online in June 2010.
• Cryptologia 1992 (Issue 2), “The Application of Sukhotin’s Algorithm to Certain Non-English Languages” by George T. Sassoon, in which he applies Sukhotin’s vowel-finding algorithm to a number of languages, including Goergian, Croatian, and Hebrew, et al. This was republished online in June 2010.
• Cryptologia 1992 (Issue 3), “A Comparison of Vowel Identification Methods” by Caxton C. Foster, in which he compares four methods of vowel identification. This was republished online in June 2010.
• Cryptologia 1997 (Issue 1), “The Distribution of Signs c and o in the Voynich manuscript: Evidence for a Real Language?” by Jacques B. M. Guy, in which he references Currier A and B and builds on the Sukhotin identification of c and o as vowels and speculates as to whether they might represent o and e, “which they resemble in shape”, “a phenomenon similar to that shown by Standard English and Scots English…”. This was republished online in June 2010.

There isn’t room to analyze all these papers in a single blog, so I will confine this article to vowel identification. Sukhotin’s algorithm is given by Guy in the first paper as follows:

“Given a text in a supposed unknown language written in some alphabetical system, Sukhotin’s algorithm identifies which symbols of the alphabet are likely to denote consonants and which vowels.”

Guy then illustrates glyph-assignments in W. F. Bennett’s transcription system from the 1970s from which his own glyph-assignments are derived:

As you can see, it’s very similar to the current EVA system.

Guy then illustrates his transcription system, which is very similar to Bennett’s, except the VMS double-cee shape is acknowledged, and some ligature-like VMS glyphs are transcribed as single characters (a decision that can be debated but may not have a significant impact on vowel-analysis statistics):

Is the Above Research Based on a Flawed Premise?

Guy’s research into VMS vowels, and that of many others, neglects important co-relationships in VMS glyphs. It’s not enough to come up with a transcription alphabet and then run frequency analysis software on individual glyphs (whether it is specific to vowels or not) if there is evidence of biglyphs or positional dependence.

Many researchers accept the spaces in the VMS as word boundaries and, for the most part, assume 1-to-1 correspondences between alphabetical letters and glyphs perceived to be vowels (either by humans or by the software). Guy does not acknowledge biglyphs in any significant way other than VMS “cc”, which has a historical precedent in early Medieval Latin texts of representing the vowel “a”.

Side note: In early medieval text, “cc” usually stood for “a”, but if “cc” was superscripted, the vowel “u”  was usually intended. The “cc”=”u” is not mentioned in Guy’s paper, he only references “a” and may not have known medieval Latin well enough to know that “cc” could also stand for “u” or the consonant “t”. He does note, on page 210, that what we call EVA-e “is always followed by {t}” but he’s referring to EVA=ch, not the “c” shape in general, which is followed by a number of glyphs.

Guy must have been working from a flawed transcript because he acknowledges “cc” and “ccc” but completely neglects “cccc”, a pattern that unambiguously occurs a number of times in the VMS, but which is almost entirely ignored in most transcripts (including the popular Takahashi transcript). But even this may not be a significant hindrance to analyzing text patterns.

A perplexing statement in Guy’s paper is that he acknowledges the ligature-like nature of some of the VMS glyphs but then partially negates this by stating: “It is certain, then, that {ct} and {et} represent single letters.” By “ct” and “et”, he is referring to EVA-ch and EVA-sh and I think there are many who would debate the certainty of this assertion.

Pairing-Patterns in VMS Text

I have described glyph co-relationships in previous blogs, including biglyphs, Janus pairs, positional constraints, and the “rules” for reproducing samples of VMS text from a conceptual basis and with examples, but this time I have decided to keep it simple and use just one glyph to get the message across in a more explicit way.

As an example of co-relationships that could significantly alter the results of computational attacks, I will refer to the backleaning glyph expressed in most transcripts as the Latin letter “i” (this glyph also appears on the third line of folio 116v in the middle of a word that resembles Latin “vix”, but this appears to be an exception).

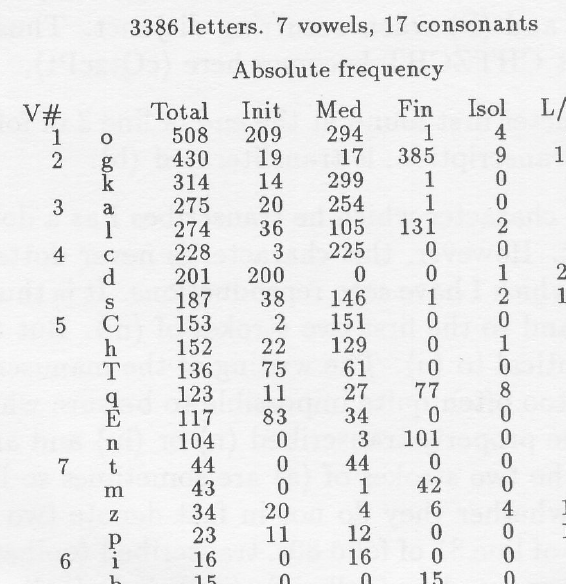
Guy analyzed two different transcripts and, in his results charts, identifies the “i” glyph as vowel #6.

Here is a detail-clip of Guy’s results from one of the transcripts he used for analysis. The chart was published in Cryptologia, 1991, Issue 3, p. 211. Glyphs that have been statistically analyzed as candidates for vowels are listed in the left-hand column. You can see quite clearly that EVA-i appears only in the medial position:

The Crux of the Matter

The problem with analyzing (or perceiving) the “i”-glyph as a vowel (or any individual letter) is that it is only positioned in one way in the VMS.

This is in stark contrast to natural languages, where vowels are found in many positions, both 1) in relation to other letters and 2) within a word.

I call EVA-i the “pivot” glyph due to its position in tokens and the way specific glyphs precede or follow it and I have not been able to find any natural language in which any vowel is always preceded by the same letter, and is always in the medial position, as in the VMS. This is why I constantly refer to the “rule-based” and “positionally constrained” nature of VMS text.

Looking More Closely at the Rules for EVA-i

With the exception of folio 116v (which may be marginalia in another hand), the backleaning-i cannot stand alone and must be preceded by “a”. It can only be followed by certain specific glyphs or glyph-groups.

VMS “i” differs from “o” and “a” (identified as vowels #1 and 3 in Guy’s chart) in that “o” and “a” can be paired with other glyphs and can move around somewhat (and can appear at the beginnings of tokens), whereas the “i” glyph cannot.

Before one argues that “i” can be preceded by another “i”, consider this…

The minims that appear after “ai” in “dain” are commonly transcribed as “n”, “m”, “v”, and there are many places in the VMS where the scribes have written them with a curved connector similar to the shape “u” (in contrast to most glyphs in the VMS, which are not connected), so the general feeling is that the minims that follow “ai” are not necessarily additional “i” shapes. Guy also acknowledges this ambiguity on page 210, and Bennett  transcribes the minims as “m”, “n” or “u”.

After going through every glyph in the VMS numerous times when I was creating my transcripts, I record them as follows:

The glyph-pair “ai” occurs almost 6,000 times in the VMS. If you run the numbers on popular transcripts, you may get different results, because the distinction between minims is not recognized in many of them (as discussed in the above chart).

But even if the minims are interpreted in a completely different way from the way I have drawn them above, even if one supposes all the minims are the same glyphs, the essential problem remains… the minims, as a group, must be preceded with “a” and do not occur at the beginnings of tokens, only together, and only at the end. The argument for “i” being a vowel becomes even weaker!

Guy acknowledges the possibility that the “i” strokes might be minims (or something else), but nowhere does he address the important fact that however one transcribes them, individually or as a group, “a” must precede them and they are never at the beginnings of words. These characteristics, taken together, are why we must question their interpretation as vowels.

Summary

Early researchers like Bennet and Guy were working with low-resolution B&W photostats, so some of their misconceptions can be forgiven, but ignoring glyph-placement is hard to excuse. Even if you can’t see fine details of individual letters, there’s no mistaking the following properties of EVA-i:

• EVA-i is virtually always preceded by “a” (there are 7 rare instances (only 1/10th of 1%) of an “r”being inserted between two minims and one is especially strange as it is in different handwriting, is out of line, and is proportioned differently),
• EVA-i never appears at the beginnings of words,
• EVA-i rarely appears at the ends of words unless all the minims are assumed to be the same, and then they are always at the end, and
• only certain specific glyphs follow “i” (I’ll include further details in a future blog).

The only way to resolve “i” into a natural-language vowel is to consider additional ways in which the text might be manipulated (as examples one would have to manipulate spaces, letter-order, or assign the same letter to multiple glyphs, or perhaps assume there are “hidden” minims, which is starting to stretch things a bit far, etc.). As it stands, if the spaces and letter-arrangement are taken as literal, and the glyph-assignments are considered consistent throughout the document, there’s not much evidence to support EVA-i as a vowel using the form of analysis proposed by Guy.

One might try to relate ai to “qu” in the sense that they are often found together and “q” rarely exists without “u”, but “qu” occurs in many different locations in a word, as can most common pairs of letters in most languages. The analogy doesn’t hold.

The Consequences

The behavior of EVA-i also affects the interpretation of EVA-a. If “ai” turns out to be a biglyph, then other instances of “a” have to be evaluated separately from “a” + “i” and the statistics will change, as will the number of glyphs that form the Voynichese “alphabet”. If there are other biglyphs (which I believe there are, as described in my blog about Janus pairs), then all the single-character computational attacks and early “vowel-assignment” research needs to be re-visited.

If, on the other hand, “ai” is not a biglyph, EVA-i is still problematic because one has to ask, “What is the purpose of the preceding “a”? or of “i” itself?” It’s possible that neither EVA-i, nor some instances of EVA-a, are vowels. They might not even be letters, but even if they are, they can not be statistically evaluated without taking into consideration the relationship of “i” to its companion.

J.K. Petersen

Copyright © 2018 J.K. Petersen, All Rights Reserved